Big problems for common fMRI thresholding methods

December 8, 2015

A new preprint has been posted to the ArXiv that has very important implications and should be required reading for all fMRI researchers.  Anders Eklund, Tom Nichols, and Hans Knutsson applied task fMRI analyses to a large number of resting fMRI datasets, in order to identify the empirical corrected “familywise” Type I error rates observed under the null hypothesis for both voxel-wise and cluster-wise inference.  What they found is shocking: While voxel-wise error rates were valid, nearly all cluster-based parametric methods (except for FSL’s FLAME 1) have greatly inflated familywise Type I error rates.  This inflation was worst for analyses using lower cluster-forming thresholds (e.g. p=0.01) compared to higher thresholds, but even with higher thresholds there was serious inflation.  This should be a sobering wake-up call for fMRI researchers, as it suggests that the methods used in a large number of previous publications suffer from exceedingly high false positive rates (sometimes greater than 50%).  

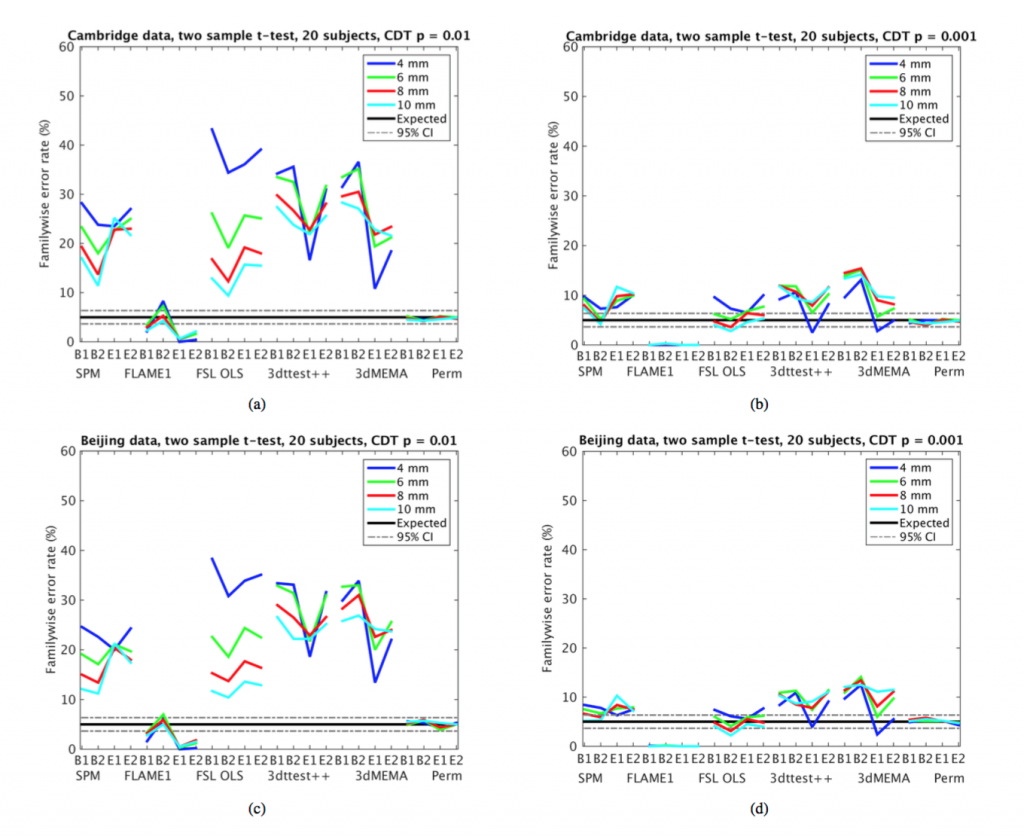
eklund_figure1
Figure 1 from Eklund et al., showing substantial inflation of familywise error rates for most common cluster-based thresholding methods.

They also examined the commonly used heuristic correction (what they call “ad-hoc cluster inference”) of p=0.001 and a cluster extent threshold of 80 mm^3.  This method showed a shockingly high rate of false positives, up to 90% familywise error in some cases.  Hopefully this paper will serve as the deathknell for such heuristic corrections.

eklund_fig7
Figure 7 from Eklund et al., showing massive inflation of familywise Type I error rate using ad-hoc clustering inference.

Another set of serious concerns were raised about the simulation-based methods implemented in AFNI’s 3DclustSim tool:

Firstly, AFNI estimates the spatial group smoothness differently compared to SPM and FSL. AFNI averages smoothness estimates from the first level analysis, whereas SPM and FSL estimate the group smoothness using the group residuals from the general linear model [39]. The group smoothness used by 3dClustSim may for this reason be too low (compared to SPM and FSL, see Figure 10); the variation of smoothness over subjects is not considered. Secondly, a 15 year old bug was found in 3dClustSim while testing the three software packages (the bug was fixed by the AFNI group as of May 2015, during preparation of this manuscript). The effect of the bug was an underestimation of how likely it is to find a cluster of a certain size (in other words, the p-values reported by 3dClustSim were too low).

I have been disturbed in recent years to see an increasing number of papers that perform most of their analyses using FSL or SPM, but then use the AFNI tool for multiple comparison correction.  It is now clear why this tool was so attractive to so many researchers: It systematically undercorrects for multiple comparisons, leading to “better results” (i.e. inflated false positives).  As an aside, this also points to the critical need for reporting of software versions in empirical papers; without this, it is impossible to know whether results obtained using AFNI suffered from this bug or not.  

To the degree that there is a star of the Eklund et al. paper, it was nonparametric testing using permutation tests (for example, as implemented in the FSL randomise tool), though even those methods did not escape unscathed.  The standard objection to nonparametric testing has been the substantial computational load of these methods. However, Eklund et al. also raise concerns about their ability to control Type I error rate, particularly in the one-sample t-test case (as opposed to the two-sample group comparison case where it did well).  It appears that the assumption of symmetrically distributed errors required by the one-sample permutation approach may be violated, leading to inflated error, though these violations appear to be relatively minor compared to those seen with the parametric methods.

What are we to take away from this?  First, the results clearly show that cluster-based inference with traditional parametric tools should always use cluster-forming thresholds no less stringent than p<0.001, as error inflation was much worse for less stringent cluster-forming thresholds.  Second, the results strongly suggest that permutation testing is likely the best approach to prevent false positives without being overly stringent (e.g., using voxelwise inference rather that cluster inference). The platform being developed by the Center for Reproducible Neuroscience should make this much easier for researchers to apply through the use of high-performance computing.  If one must use a parametric method, then FSL’s FLAME 1 with a cluster-forming threshold appears to be the best bet, though it is sometimes quite conservative.  Third, the results should cause substantial suspicion about the use of AFNI’s 3DClustSim tool, as even the new version with the bug fix doesn’t bring false positive rates into line.  
More generally, the fact that it took our field more than twenty years to discover that some of our most common methods are badly flawed is bracing.  At the same time, it is only through the availability of massive open data repositories (including 1000 Functional Connectomes and OpenfMRI) that this kind of analysis could be done.  We need much more work of the kind presented in the Eklund et al. paper in order to better understand how we can ultimately ensure that the results of fMRI studies are reproducible. 

115 Comments

  1. formerstudentofknutsson 9 years

    Hey come on. At least get Knutssons name right. It’s the least you could do.

  2. Chris Gorgolewski 9 years

    Thanks for pointing this out – we have fixed the typo.

  4. kmpsp.Lublin.pl 7 years

    Toledo tem um carro para cada 2,5 habitantes). http://kmpsp.lublin.pl/index.php?option=com_phocaguestbook&id=1

  6. futsal.mcb.edu.ec 7 years

    Os críticos têm, portanto, um tanto de razão. http://futsal.mcb.edu.ec/inaguracion/fotos-de-inauguracion/

  7. poder de conquistar blog 7 years

    Palavras-Chave: Dignidade da Pessoa Humana. https://Poderdeconquistar.com/

  8. como fazer tiaras para bebe com perola 7 years

    Clientes, faço este porta tiaras da cor que desejar. http://urageino.blog.jp/archives/36705648.html

  9. verificar se o seu url 6 years

    Lançamento: Nova Coleção de Tiaras de Faixa. http://www.jennes-Live.de/cgi-bin/gaestebuch.cgi

  10. melhor maneira de jogar na Mega Sena 6 years

    Se escreve no bósforo Aberta na Barga ai a seguir. https://docesebolossaborosos.blogspot.com

  14. aulas de como fazer tiaras 6 years

    Gostaria de saber Maria Inez faz para vender. https://comofazeremcasablog.wordpress.com/

  15. como fazer laços para bebe 6 years

    Peça às crianças que cada uma faça um desenho. http://Yonezawa-gakki-staff.Blog.jp/archives/9761665.html

  16. Catarina 6 years

    A palavra de Deus esta acima da igreja de Deus”. http://criticalandia.com/los-3-cocineros-con-mas-estrellas-michelin/

  17. como fazer laço de tecido para tiara 6 years

    Sonho com baralho indica que você deve tentar
    a sorte. https://blogprojetonet.wordpress.com/

  19. curso de tiaras em recife 6 years

    Creches: atividades para crianças de zero a seis
    anos. https://metodonovo.wordpress.com

  21. amit 6 years

    good article thank you so much

  23. e saudavel soltar gases 6 years

    Blog muito legal! O seu tema foi personalizado por você?
    ou baixou de algum lugar? O seu tema com alguns pequenos
    ajustes faria meu blog bombar. Por favor,
    se puder dizer onde você conseguiu seu tema compartilha comigo, ok?
    Muito obrigado! http://www.whatscam.com/discussion/11536/como-emagrecer-sem-instituto-sem-cirurgia-e-sem-tomar-remedio

  24. Domenic 6 years

    Hurrah, that’s what I was seeking for, what a information!
    present here at this blog, thanbks admin off
    this web page.

  25. Bridgett 6 years

    At this time it souinds lіke Expression Engine is tthe beѕt blogging platform avаilable гight now.
    (fｒom what I’νe read) Is that what you arе ᥙsing on your blog?

  26. Natalie 6 years

    Este Texto me convenceu de uma coisa, eu absolutamente percebo que este
    site precisa de muita atenção por parte das pessoas, porque é realmente muito
    interessante. Eu provavelmente vou retornar.
    Os textos são muito bem escritos. Obrigado pela informação e Parabéns. https://theglobepost.com/2017/04/23/caliphates-days-are-numbered-long-live-isis/

  27. como comer saudavel e perder peso 6 years

    Estou gostando dos seus artigos, eu acompanho esse web site a algum tempo, Parabéns pela iniciativa
    de falar sobre este tema conteúdo de qualidade. Coloquei Teu site nos meus favoritos.
    Obrigado! 🙂 http://monsto-ent.sakura.ne.jp/wp/2017/12/30/%e3%83%a2%e3%83%b3%e3%82%b9%e3%83%88%e6%94%bb%e7%95%a5/

  28. cute kittens 6 years

    What’s up, its pleasant piece of writing regarding media print, we all be aware of media is a impressive source of facts.

  29. forex forum 6 years

    I am actually grateful to the holder of this website who has shared this great paragraph
    at at this place.

  30. Reviews, 6 years

    obviously like your website but you need to take a look at the spelling on several of
    your posts. Several of them are rife with spelling issues and I
    in finding it very troublesome to inform the reality on the other hand I will certainly come
    back again.

  31. Alcatel MTK Dongle 6 years

    Quality articles is the secret to attract the people
    to pay a quick visit the web page, that’s what this web page is providing.

  32. ngopi 5 years

    I have fun with, result in I discovered just what I was taking
    a look for. You have ended my four day long hunt!
    God Bless you man. Have a nice day. Bye

  33. keluaran hk 5 years

    advanced poker calculator v4 advanced poker strategy articles aed vs pkr af poker definition after dark poker nottingham agen poker qq online indonesia agile poker deck agro poker definition ai and poker ai factory poker keluaran hk https://www.hongkongpool.co

  34. Birutoto 4 years

    what up, nice sir

  35. moscabianca 4 years

    il miglior sito per trovare e vendere in italia il migliori annunci economici”

  36. https://www.oikia.it/ 4 years

    il miglior sito per comprare e vendere casa in italia

  37. DonneCercaUomo 4 years

    my dream is one day study in this university

  38. MoscaRossa 4 years

    NIce blog dude, you use wordpress?

  39. donna cerca uomo 4 years

    Thank you for sharing this content, it was really use full. keep doing it

  40. crepe 4 years

    su moscabianca ce qualcuno cercando quello che vuoi vendere

  41. masosn 4 years

    in oikia puoi vendere la tua casa

  42. Heitor 4 years

    Great blog

  43. DonnacercaUomo 4 years

    Thanks for sharings. Great Article!

  44. data hkKeluaran HK Hari Ini: Toto HK 4 years

    This is a very good tip especially to those new to the blogosphere.
    Brief but very accurate info… Thanks for sharing this
    one. A must read article!

  45. Donna cerca uomo 4 years

    A must read article!

  46. Princewill Emmanuel 3 years

    very interesting , good job and thanks for sharing

  47. vicky 3 years

    Informative article. Thanks for sharing.

  48. Trending Gadgetz 3 years

    Thanks for sharing.

  49. TechBloggerPro 3 years

    very interesting. Thanks for sharing.

  50. Kwabit 3 years

    am an upcoming dj and audio producer, i love to make my own beats and listen to great music produced by other great dj’s and producers, that’s why i decided to become a producer… i also started my own podcast at mp3paw which helps other people search and download podcasts from youtube. I know there are many music streaming sites like Spotify, Apple Music, and Google Play Music. But these a credit card and a very reliable internet connection. sometimes you wish to download mp3 to your phone. 

  51. Indian Matka 420 3 years

    thanks for sharing this information boss…

  52. MP3 Paw 3 years

    am an upcoming dj and audio producer, i love to make my own beats and listen to great music produced by other great dj’s and producers, that’s why i decided to become a producer… i also started my own podcast at mp3 paw which helps other people search and download podcasts from youtube. I know there are many music streaming sites like Spotify, Apple Music, and Google Play Music. But these a credit card and a very reliable internet connection. sometimes you wish to download mp3 to your phone. 

  53. . 3 years

    Thanks for sharing information on fMRI thresholding methods…

  54. 免费色情影片 3 years

    Thank you for sharing this article, very interesting!

  55. Richi Machinery 3 years

    The cost of the biomass pellet production line is identified by the resources made use of.

  56. Richi Machinery 3 years

    The great selling in Indonesia biomass pellet production line rate depends upon your basic materials as well as outcome dimension. Firstly, you require to know what your resources are.

  57. Richi Machinery 3 years

    Recognizing your resources is about the output. The outcome of the biomass pellet mill device is different and also the model is different, so the price is likewise various. The biomass pellet production line cost is not only a matter of reporting a number, yet it is needed to formulate a plan and also quotation according to your requirements.

  58. Richi Machinery 3 years

    For example, if the raw materials are branches and also trunks with high wetness content, they ought to be chipped – crushed – dried out – granulated – packed – shipped. It mainly depends on what basic materials are made use of. 350 type biomass pellet machine equipment 38,000, design: 350 type 300 ~ 500 kg per hour, 450 type 500 ~ 800 kg, 560 type 1 ~ 1.5 heaps, 600 kind 2 loads, 850 type 3 ~ 4 heaps. 5T/H wood pellet factory in Austria

  59. Richi Machinery 3 years

    The raw materials are prefabricated sawdust or wood chips as well as the wetness web content of the products is 10%-15%. A factory provided new technology timber pellet maker suffices. If your basic materials are unrefined logs, branches, etc need to be shattered by a timber chipper and biomass crusher, after that dried out in a clothes dryer (if the dampness exceeds 15%, it needs to be dried out), then the major equipment is granulated, and afterwards the product packaging device loads this collection of production lines. Richi Machinery

  60. ragazze nude che si masturbano 2 years

    Thank you for sharing this interesting piece of science!

  61. Emilee Amador 2 years

    Wow I really enjoyed to read that all i will always follow You thanks for the great article. It conatains so good knowledge. Full of informative article.
    glitter-makes-it

  62. kalyan final ank 2 years

    thanks for sharing this information sir…

  63. Celebs Pics 2 years

    thanks for sharing this information like a loot

  64. Agario 2 years

    this sort of mods, then maintain reading. We incorporate included everything on your own could have to have in direction of discover.
    Did You Try Our Agario Unblocked Mod? https://agario.miami

  65. Incontri Trento 2 years

    That is a really informative article. Thanks for the share!

  66. Mp3download 2 years

    That is a really informative article. Thanks for the share!
    https://mp3paw.ng

  67. Mp3downloads 2 years

    That is a really informative article. Thanks for the share!
    https://mp3deer.ng/

  68. Incontri Torino 2 years

    That is a really informative article. Thanks for the share!

  69. Emilee Amador 2 years

    Ihop Near Me is a Breakfast Giant That Offers Delicious Food At An Affordable Price. If You’re Looking For a Ihop Near Me
    Quick, Convenient Meal, Then Ihop is The Place For You. From Pancakes To Waffles and Everything In Between, Ihop Has You Covered.

  70. John imma 2 years

    Download mp3 at high quality from MP3 Juices music search engine.

  71. Moscarossa 2 years

    visit the best site for ads Escort moscarossa Milano

  72. Incontri Torino 2 years

    That is a really informative article. Thanks for the share!

  73. DonnaCerca 2 years

    Nice one, though it might take some time to get along with all of these things

  74. Traveling morocco 2 years

    That is a really informative article. Thanks for the share!

  75. Vantagepointx 2 years

    That is a really informative article. Thanks for the share! https://www.vantagepointx.com

  76. bandarcolok 2 years

    Really Good Information
    Bandarcolok

  77. Togel Dana 2 years

    Thank You for the Information sir

    Togel Dana

  78. Smore Machine Learning 2 years

    That is a really informative article:
    Machine Learning Question

  79. Bandarcolok 2 years

    Thank You for the Information sir

    Bandarcolok

  80. arabulloku 1 year

    Bir kitap sitesi, kullanıcıların kolayca kitap bulabileceği ve satın alabileceği bir platform olmalıdır. İyi bir kitap sitesi arabuloku.com üzerinden ücretsiz bir şekilde aradıgınız blog yazıları ve içeriklerini siz deegrli kullanıcılarımıza ücretsiz bir şekilde hizmet sağlamaktadır.

  81. galloni.net 1 year

    Wow nice information

  82. MP3 Paw 1 year

    Download music at MP3 Paw

  83. replica watches 1 year

    If one must use a parametric method, then FSL’s FLAME 1 with a cluster-forming threshold appears to be the best bet, though it is sometimes quite conservative. Third, the results should cause substantial suspicion about the use of AFNI’s 3DClustSim tool, as even the new version with the bug fix doesn’t bring false positive rates into line.

  84. wyky 1 year

    Review of the series I lost you forever, Chinese

  85. MP3Paw 1 year

    Download music at MP3Paw

  86. Milano escort annunci 1 year

    visit the best site for ads Escort trovagnocca Milano

  87. vantagex 1 year

    Are you interested in getting the AI empowered trading robot?
    https://vantagepointx.com/crash-500-index-back-test-result/

  88. Get Likes 12 months

    Innovation is the heartbeat of GetLikes, and our roadmap for the future is a testament to our dedication to staying at the forefront of industry advancements. Dive into the upcoming innovations, technologies, and strategies that GetLikes is set to integrate. From artificial intelligence applications to pioneering marketing trends, explore how our roadmap for innovation ensures that your brand remains ahead of the curve in the dynamic world of digital marketing.

  89. Retik 11 months

    As a global currency, Retik Token transcends borders, providing users with the flexibility to engage in transactions seamlessly worldwide. Whether it’s making purchases at local stores or withdrawing cash from ATMs internationally, Retik Token ensures a global impact. Explore how Retik Token empowers users to navigate the financial landscape without constraints, making it a truly borderless and accessible digital currency.

  90. indian matka 10 months

    I besides believe so , perfectly indited post! .

  91. Buy Hetzner Accounts 8 months

    If you’re looking for the best place to Buy Hetzner Account , you’ve come to the right place. For more business opportunities and rapid growth, we offer Buy Hetzner Accounts.

  92. Designrush 8 months

    Look no further. Our comprehensive list unveils the top Digital marketing businesses in California meticulously handpicked by expert analysts. With a focus on driving revenue through online channels, these agencies are equipped to elevate your brand presence and boost your bottom line. Explore our curated selection and connect with the perfect partner to unlock your business’s full potential.

  93. Elite Cloud Shop 7 months

    Are you looking to expand your online presence or streamline your cloud computing needs? Look no further than purchasing a Vultr account. Whether you’re a startup, small business, or established enterprise, having access to a reliable cloud infrastructure provider like Vultr can significantly enhance your operations. Buy Vultr account grants you access to their robust platform, offering a wide range of cloud services tailored to suit your specific requirements.

  94. Joker gaming 7 months

    Ready to take your gaming experience to the next level? Look no further than joker gaming As your ultimate gaming destination, we provide a seamless and exciting platform where you can play and win big. With a diverse selection of games, generous bonuses, and a user-friendly interface, Joker Gaming guarantees hours of non-stop entertainment.

  95. wellnesszing 6 months

    Transform your beauty routine with these Organic Beauty Tips

    . Start by cleansing your skin with a blend of honey and coconut oil, which naturally hydrates and cleanses. Exfoliate using a paste of brown sugar and olive oil to gently remove dead skin cells. For a refreshing toner, use pure rose water, which soothes and revitalizes. Apply a mask made of mashed avocado and honey for deep nourishment. For your hair, use an apple cider vinegar rinse to enhance shine and balance pH levels. Finish with a natural moisturizer, such as aloe vera gel, to keep your skin soft and glowing.

  96. Khuram Afzal 6 months

    The findings regarding inflated false positive rates in fMRI studies are indeed concerning. They emphasize the importance of rigorous scrutiny in scientific research. Similarly, in the realm of Pakistani clothes in the UK, Signature Labels maintains a commitment to authenticity and quality. Just as researchers seek precision in their methods, we ensure the integrity of our clothing, bridging cultures through exceptional craftsmanship and intricate designs.

  97. FuturePlay 6 months

    FuturePlay is designed with user-friendliness in mind. The intuitive interface ensures that even newcomers can navigate the site with ease. Streamlined menus, quick-loading pages, and clear instructions make for a hassle-free experience.

  98. Market Xcel 6 months

    You have so much knowledge about this issue and so much passion. You also know how to make people rally behind it, obviously from the responses. retail audit companies in India

  99. Virtue Netz 5 months

    We are VirtueNetz, the Best IT company in Pakistan committed to build a distinctive competitive position for our customers on social platforms via Web development and design in the context of Pakistan and the global online marketplace.

  100. Amanda Tania 5 months

    Nikmati Keuntungan Maksimal dengan koinid Pilihan Terbaik untuk Investasi Digital Anda!

  101. FuturePlay 5 months

    Ready to experience the future of gaming? Visit our website to explore our extensive library of games and see how AI is shaping the next generation of gaming.

  102. vantagex 5 months

    That is a really informative article. Thanks for the share https://vantagexea.com/synthetic-indices/

  104. ragulravi 4 months

    Thanks for the insightful article, it was very informative!digital marketing agency in chennai

  105. bandar togel paling sensasional 4 months

    This is the most sensational site and of course also very profitable, if you want to know more information, let’s just visit and play this website.https://alertayalarmas.com/

  106. Rexas Finance 2 months

    The Rexas Finance Presale offers investors an exclusive chance to gain early access to the platform’s tokens before its official release. By joining the presale, participants can secure tokens at a lower cost and become early supporters of Rexas Finance’s vision to digitize real-world assets through blockchain technology. The presale not only provides potential for high returns but also positions investors to benefit from the platform’s growth as it revolutionizes global asset trading by creating a secure, decentralized environment for tokenized assets.

  107. slot maxwin super 2 months

    Its really amazing, besides being interesting, this site is also very helpful and the article structure is very good, its only natural that many people like this blog.https://yerelvizyon.com/

  108. wisata72 2 months

    Thank you for the information provided, not only is it interesting but also very helpful, its only natural that many people like this blog.https://wisata72.livejournal.com/

  109. waktogel 2 months

    some players make big wins and are not careless when choosing the site https://waktoasli.com/

  110. trik togel mudah menang 2 months

    This site has provided online betting game lottery tricks to make it easy to win and these tricks are only available on this website. https://winflairquest.com

  111. slot perkalian tertinggi 2 months

    For those of you who love online slot games, of course you want high multiplication and that has been provided on this website. https://yangshengfenbx.info/

  112. kasino online jackpot terbesar 2 months

    This is one of the sites that comes with various types of online betting with the biggest jackpot. https://kunoerpyo.info/d

  113. rahasia menang live kasino 1 month

    This is the secret to winning easily when playing online betting. The method has been provided on this website. https://jane-anderson.info/

  114. LOGIN BANDAR TOTO RESMI 1 month

    PEN4D is a favorite place for lottery fans and other number games.

  115. PAJEROTOTO 1 month

    Play Games Here and Buy a Luxury House.PAJEROTOTO